To derive a method for drawing all types of lines, let's first start with the simple lines. These will be the horizontal and the vertical lines. Let's see what properties that each of these have.

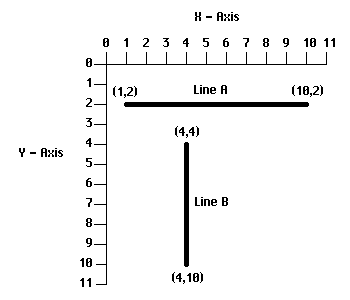
To derive a single algorithm that can draw both of these lines, as well as the sloped lines, we must examine what makes up each line. Lines consist of two point of reference, coordinates (X1, Y1) and (X2, Y2). From these values, we can get two more values, delta X and delta Y. These delta values are very important for determining the angle (slope) of the line. In algebra, every value for Y has a unique value for X. Looking at "Line A" we can determine that the slope is 0 and therefore a horizontal line. The slope for "Line B" is undefined, whenever a line's slope is undefined we can determine that the line will be vertical. Here's how I figured that out, the formulas (or the algorithm) for determining the slope of a line are as follows:
First, determine the delta values.
delta X = X2 - X1
delta Y = Y2 - Y1
The slope (m) is equal to the ratio of both deltas.
delta Y
m = -------
delta X
The slope is the increment for the Y coordinate. For every increment of 1 on the X value of 1, the value of the slope (m) is added to the current Y coordinate. Let's look at the horizontal line "Line A." We can determine its slope like so:
Line A = (1, 2) - (10, 2)
therefore: X1 = 1 X2 = 10
Y1 = 2 Y2 = 2
delta X = 10 - 1 = 9
delta Y = 2 - 2 = 0
delta Y 0
m = ------- m = --- m = 0
delta X 9
We determine that the slope (or Y increment) of the line is 0. Is this accurate? For every increment of the X value by 1, zero is added to the Y value along the line. Looks pretty accurate to me.
"Line B" is a vertical line; if we tried to determine its slope we'd end up with infinity for the value of m (or an undefined value). This is because X1 and X2 are equal in value (both are equal to 4). So the value for delta X would be zero since delta X equals to X2 minus X1. If we tried to get the slope, we'd find that:
Line B = (4, 4) - (4, 10)
therefore: X1 = 4 X2 = 4
Y1 = 4 Y2 = 10
delta X = 4 - 4 = 0
delta Y = 10 - 4 = 6
delta Y 6
m = ------- m = --- m = infinity
delta X 0
This means that for every increment of the X value, the slope (m) is added to the Y value. In this case, delta X is zero, so the X value never gets incremented, and since the slope is infinity, infinity is added to the Y value. Um, well, beleive it or not, this is really accurate considering that the line is totally vertical. However, there would be no way to actually calculate the value for infinity, so we must come up with a rule. The rule is simply this: if X1 and X2 are equal, draw the line vertically (the same way that the 'DrawVertLine' function does).
We could write pseudocode to kind of get an idea on how to put this algorithm into a C function, but this should not be too complicated so I will just go ahead and write the code for it. Here's what our line function looks like so far:
/* Line function:
*
* Draws a line given 2 (X,Y) coordinates and a color attribute.
*/
void Line(int X1, int Y1, int X2, int Y2, unsigned char C)
{
int i; /* Loop counter and temp variable */
float deltaX, deltaY; /* 2 deltas */
float slope, currY; /* slope and current Y coordinate */
if (X2 == X1) { /* determine if line is vertical */
/* If so, draw vertical line */
if (Y1 > Y2) {
/* smallest value first please */
i = Y1; Y1 = Y2; Y2 = i;
}
/* draw vertically from Y1 to Y2 */
for (i = Y1; i <= Y2; i++)
SetPixel(X1, i, C);
} else {
/* determine slope, if not vertical */
if (X1 > X2) {
/* smallest value first please */
i = X1; X1 = X2; X2 = i;
i = Y1; Y1 = Y2; Y2 = i;
}
/* get the two deltas and the slope */
deltaX = X2 - X1;
deltaY = Y2 - Y1;
slope = deltaY / deltaX;
/* draw the line */
currY = Y1;
for (i = X1; i <= X2; i++) {
SetPixel(i, (int)currY, C);
currY += slope;
}
}
}