|
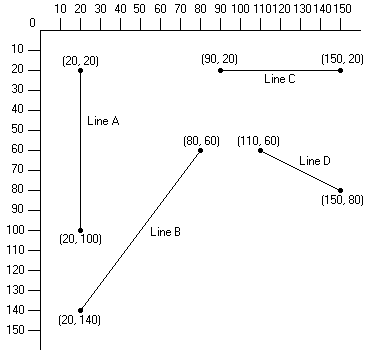
Now it's time to put this function to the test. To use it, let's try some examples. Let's have the function draw the following lines.

|
We'll draw these lines using the following statements:
Line( 20, 20, 20, 100, 1); /* Line A */
Line( 20, 140, 80, 60, 2); /* Line B */
Line( 90, 20, 150, 20, 4); /* Line C */
Line(110, 60, 150, 80, 7); /* Line D */
And you will see 4 perfectly drawn lines on the screen. But if you notice, line B looks broken compared to the other 3 lines. This is because the Y coordinates are skipping pixels for each iteration in the loop that draws the line. To see why, let's look at the math behind this line.
Line B - (20, 140) - (80, 60)
(X1, Y1) - (X2, Y2)
delta X = X2 - X1 delta Y = Y2 - Y1
delta X = 80 - 20 delta Y = 60 - 140
delta X = 60 delta Y = -80
delta Y -80
slope = ------- slope = ----- slope = -1.33
delta X 60
For this particular line, each increment on the X coordinate, Y is incremented (decremented actually) by 1 1/3. Of course, due to truncation, it isn't all that noticeable except for every 3 iterations when the 1/3's add up to a whole. That's when the Y coordinates will skip a pixel, as illustrated below:
|
Well the way to correct it is to redefine the slope for the X coordinate, instead of the Y. Let's illustrate by redoing the math for the new slope.
Line B - (20, 140) - (80, 60)
(X1, Y1) - (X2, Y2)
delta X = X2 - X1 delta Y = Y2 - Y1
delta X = 80 - 20 delta Y = 60 - 140
delta X = 60 delta Y = -80
Now note that the slope for Y is the recipricole of the slope for X.
delta X 60
slope = ------- slope = ----- slope = -0.75
delta Y -80
Now instead of incrementing the X coordinate by the constant of one, we do that for the Y coordinate. The X coordinate increments (or decrements) by the slope for every increment of the Y coordinate.
|
Now it's time to update our 'Line' function for the new algorithm, but first, we need to restate the functionality of it. This way, we can write our code as efficiently as possible. Going from that, we get the following:
Get value for delta X.
Get value for delta Y.
Check if absolute value of the slope off the X axis is > 1.
This can be done by doing the following:
If |delta Y| > |delta X| Then
If Y2 < Y1 Then
Swap values of Y2 and Y1, Y1 must be < Y2
Swap values of X2 and X1, both coordinates must be swapped.
Plot each pixel beginning at coordinates (X1, Y1)
After plotting each pixel,
increment the Y-coordinate by one and ...
increment the X-coordinate by the value of slope.
Until Y-coordinate = Y2.
ElseIf |delta Y| or |delta X| NOT = 0 Then
If X2 < X1 Then
Swap values of X2 and X1, X1 must be < X2
Swap values of Y2 and Y1, both coordinates must be swapped.
Plot each pixel beginning at coordinates (X1, Y1)
After plotting each pixel,
increment the X-coordinate by one and ...
increment the Y-coordinate by the value of slope.
Until X-coordinate = X2.
Else
Set a single pixel 'cause X1 = X2 and Y1 = Y2
Now, using this as a guideline, our function now looks like this:
/* Line function
*
* Revised line function that will draw full lines
* in any slope at any angle.
*/
void Line(int X1, int Y1, int X2, int Y2, unsigned char C)
{
float currX, currY; /* Current pixel to be plotted */
float deltaX, deltaY, slope; /* 2 deltas and slope */
int tempVal; /* Holds temporary values */
deltaX = X2 - X1; /* Get value for delta X */
deltaY = Y2 - Y1; /* Get value for delta Y */
if (deltaX < 0) deltaX = -deltaX; /* Need absolute */
if (deltaY < 0) deltaY = -deltaY; /* values only. */
if (deltaY > deltaX) {
/* |slope| > 1 */
if (Y2 < Y1) {
/* Swap coordinates, Y1 must be < Y2 */
tempVal = Y2; Y2 = Y1; Y1 = tempVal;
tempVal = X2; X2 = X1; X1 = tempVal;
}
/* Compute deltas and slope */
deltaX = X2 - X1;
deltaY = Y2 - Y1;
/* Slope off the vertical axis */
slope = deltaX / deltaY;
/* Plot each pixel starting at (X1, Y1) */
currX = X1;
for (currY = Y1; currY <= Y2; currY++) {
SetPixel((int)currX, (int)currY, C);
currX += slope; /* increment X by the slope */
}
return;
} else if ((deltaY || deltaX) != 0) {
/* |slope| < 1 */
if (X2 < X1) {
/* Swap coordinates, X1 must be < X2 */
tempVal = X2; X2 = X1; X1 = tempVal;
tempVal = Y2; Y2 = Y1; Y1 = tempVal;
}
/* Compute deltas and slope */
deltaX = X2 - X1;
deltaY = Y2 - Y1;
/* Slope off the horizontal axis */
slope = deltaY / deltaX;
/* Plot each pixel starting at (X1, Y1) */
currY = Y1;
for (currX = X1; currX <= X2; currX++) {
SetPixel((int)currX, (int)currY, C);
currY += slope; /* increment Y by the slope */
}
return;
} else
/* Set a single pixel because Y1 = Y2 and X1 = X2 */
SetPixel(X1, Y1, C);
}